공대상상 첫 화면으로 이동

드넓은 캠퍼스, 효율적인 이동은 공대생의 숙명!

서울대학교 캠퍼스는 그 광활함으로 유명합니다. 200개가 넘는 건물 안에는 각종 단과대학 연구소는 물론 은행, 헬스장, 수영장, 미술관까지 자리하고 있습니다. 관악산 속 캠퍼스는 아름다운 풍경을 선사하지만, 동시에 캠퍼스 내 이동에 큰 어려움을 주기도 합니다. "정문에서 윗공대는 걸어서 가지 말라"는 이야기가 있을 정도지만, 공대생에게 불가능이란 없죠! 넓은 서울대학교 캠퍼스의 주요 건물들을 코딩으로 탐험해볼까요?

TSP, 그게 뭐에요?

효율적으로 탐험하는 방법을 고민하다 보면, 자연스레 외판원 문제(Traveling Salesperson Problem, TSP)에 흥미를 갖게 됩니다. 외판원 문제란, 여러 지역을 도는 판매원(외판원)이 모든 지역을 돌고 다시 출발점으로 돌아와야 한다고 할 때, 최적의 경로를 찾는 문제입니다. 이는 물류 최적화¹⁾, 배송 경로 설정 등 다양한 분야에서 중요한 문제로 다뤄지고 있습니다. 이번 시간에는 서울대학교의 건물들을 둘러보는 외판원이 되어 가장 효율적인 동선을 코딩해봅시다.

TSP 문제를 해결하기 위한 다양한 알고리즘이 존재하는데요. 이번 기사에서는 몇 가지 대표적인 알고리즘을 소개하고, 이를 서울대학교 캠퍼스 건물 간 최적 경로 탐색에 적용하여 그 성능을 비교해 볼 예정입니다. 우리가 살펴볼 알고리즘은 다음과 같습니다.

이제, 본격적으로 외판원이 되어 캠퍼스를 누벼볼까요? 물론 공대생답게 효율적으로 말이죠!

1단계. 가중치 그래프, 현실의 지도를 코드로 옮기기

효율적인 경로 탐색을 위해서는 캠퍼스 지도를 기반으로 그래프(Graph)를 구성해야 합니다. 컴퓨터 과학에서 그래프란 현실 세계의 복잡한 관계를 점에 해당하는 노드(Node)와 두 점을 잇는 간선(Edge)으로 단순화한 모델입니다. 이를 서울대학교에 적용하면, 각 건물이 바로 '노드'가 되고, 이 건물들 사이를 이동하는 데 소요되는 시간이 '간선'이 됩니다.

하지만 각 건물 사이의 소요 시간 즉, 간선은 거리에 따라 달라지게 됩니다. 이때 필요한 것이 바로 각 간선에 '가중치(Weight)'³⁾ 또는 '비용(Cost)'이라는 숫자 값을 부여한 가중치 그래프(Weighted Graph)입니다. 우리의 '서울대학교 캠퍼스 탐방' 문제에서는 각 건물 사이를 도보로 이동하는 데 걸리는 '예상 소요 시간'이 바로 이 가중치가 됩니다.

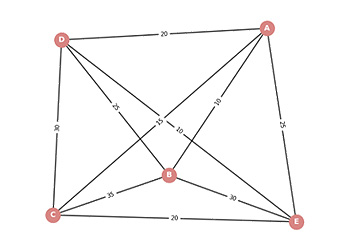
우선, 간단한 예시를 통해 그래프를 코드로 표현하는 방법을 알아보겠습니다. 위 그림은 5개의 노드로 이루어진 가중치 그래프입니다. 위 코드는 그래프를 '각 노드에 대해 연결된 노드' - '그 사이 간선의 가중치 값'을 쌍으로 순차적으로 저장한 딕셔너리⁴⁾를 정의한 것입니다.

위 코드에서 각 키⁵⁾('A', 'B', 'C', 'D', 'E')는 건물을 나타내며, 각 키에 대한 값은 다른 건물과의 연결 정보와 이동 시간(가중치)을 담고 있습니다. 예를 들어, 'A': {'B': 10, 'C': 15}는 A 건물에서 B 건물까지 이동하는 데 10분이 걸리고, C 건물까지 이동하는 데 15분이 걸린다는 의미입니다.

가중치 그래프의 기본적인 구조는 위와 같습니다. 실제 서울대학교 캠퍼스 전체에 대한 그래프는 더 많은 노드와 간선 정보를 포함하여 그래프를 시각적으로 이해하기 어렵기 때문에 기본 구조를 사용하여 알고리즘 성능 비교를 진행하고자 합니다.

2단계. 알고리즘 구현 및 성능 비교

2. 동적 계획법(Dynamic Programming): 점화식처럼, 메모로 똑똑하게 풀기!

고등학교 수학 시간에 배운 점화식을 기억하시나요? 점화식을 처음 들어보는 학생도 괜찮습니다. 점화식은 간단히 말해 '이웃한 항들 사이의 관계를 나타낸 식'으로, "다음 값은 이전 값을 이용해 이렇게 구할 수 있다"는 규칙을 의미합니다. 예를 들어, 매일 저금통에 3개씩 동전을 넣는다면, n번째 날의 동전 개수 = (n-1)번째 날의 동전 개수 + 3 이라는 규칙을 식으로 나타낸 것이 바로 점화식이죠.

동적 계획법은 바로 이 점화식의 원리를 프로그래밍에 적용한 것입니다. 즉, 작은 문제의 답을 이용해 더 큰 문제를 해결하는 전략입니다.

동적 계획법은 크게 두 가지 핵심 아이디어를 바탕으로 합니다.

• 1. 문제를 작은 단위로 쪼개기: 해결하려는 큰 문제를 여러 작은 하위 문제(Subproblem)로 나눕니다.
• 2. 계산 결과 저장하고 재활용하기: 한 번 계산한 하위 문제의 답을 메모장(Memoization)에 저장해두고, 같은 문제가 다시 나오면 저장된 답을 가져와 중복 계산을 피합니다.

외판원 문제(TSP)에 이 방식을 적용해 봅시다. 예를 들어, '정문에서 출발하여 체육관과 경영대학을 거쳐 예술관에 도착하는 최단 경로'를 찾는다고 가정하겠습니다. 이 문제를 풀려면, '정문에서 출발하여 체육관을 거쳐 경영대학에 도착하는 최단 경로'와 같은 더 작은 문제들을 먼저 풀어야 합니다.

동적 계획법은 이때 '정문 → 체육관 → 경영대학'의 최단 시간을 계산한 뒤 그 결과를 '메모장'에 기록해 둡니다. 나중에 다른 경로를 탐색하다가 이와 동일한 하위 경로가 필요해지면, 처음부터 다시 계산하는 대신 메모장에 적어둔 값을 바로 가져와 사용하는 것입니다. 아래 코드 속의 memo = {} 부분이 바로 이 메모장 역할을 합니다. 동적 계획법은 바로 이 메모장에 이미 해결한 문제의 답을 버리지 않고 차곡차곡 쌓아 나갑니다. 이를 통해 완전 탐색의 막대한 중복 계산을 획기적으로 줄여 효율적으로 최적의 해를 찾아낼 수 있는 것입니다.

그런데 컴퓨터는 '어떤 건물들을 방문했는지' 상태를 어떻게 효율적으로 기록하고 확인할까요? 이때 비트마스킹(Bitmasking) 기법이 사용됩니다. 비트마스킹은 각 건물의 방문 여부를 0과 1, 즉 하나의 비트(bit)로 표현하고 하나의 숫자로 압축해 저장하는 방법입니다. 예를 들어, 방문할 건물이 총 5개이고 그중 1번과 3번 건물을 방문했다면, 이 상태를 이진수 10100으로 표현하는 식입니다. 컴퓨터는 이 숫자를 통해 어떤 건물을 방문했고 어떤 건물을 아직 방문하지 않았는지 빠르고 효율적으로 파악할 수 있습니다. 코드에서 방문 기록을 확인하는 부분이 바로 이 기법을 활용한 것입니다.

Python
# (현재 노드, 방문한 노드 집합)을 키(Key)로, 해당 상태까지 도달하는 '최단 거리'를 값(Value)으로 저장합니다.
memo = {}

# 'A', 'B', 'C'와 같은 건물 이름을 0, 1, 2와 같은 컴퓨터가 다루기 쉬운 숫자로 바꿉니다.
# 특히, 건물의 방문 여부를 0과 1로 표현하는 '비트마스크' 기법을 사용을 위해 필수적입니다.
nodes_map = {node: i for i, node in enumerate(nodes)}

# tsp_dp 함수: 동적 계획법으로 TSP 문제를 푸는 핵심 재귀 함수
# - graph: 전체 건물 간의 거리 정보가 담긴 그래프
# - current_node_idx: 현재 위치한 건물의 번호(인덱스)
# - visited_mask: 지금까지 어떤 건물들을 방문했는지 비트(0과 1)로 기록한 값
def tsp_dp(graph, current_node_idx, visited_mask):
    # [재귀의 종료 조건]
    # 모든 노드를 방문시 현재 위치->출발점 거리만 반환 후 종료합니다.
    if visited_mask == (1 << len(nodes)) - 1:
        start_node_name = nodes[0]
        current_node_name = nodes[current_node_idx]
        return graph[current_node_name][start_node_name]

# 메모이제이션: 계산 결과를 저장해두고 다음에 같은 계산을 다시 하는 대신 저장해둔 값을 가져다가 쓰는 기법
if (current_node_idx, visited_mask) in memo:
        return memo[(current_node_idx, visited_mask)]

    # 아직 계산된 적 없는 문제라면, 최소 비용을 무한대(가장 큰 값)로 초기화합니다.
    min_cost = sys.maxsize

# 방문하지 않은 다음 노드로 이동합니다.
for next_node_idx in range(len(nodes)):
    # 비트 연산(&)으로 next_node_idx에 해당하는 건물 이미 방문했는지 확인
    if not (visited_mask & (1 << next_node_idx)):
        # 다음 목적지까지의 경로 비용을 재귀적으로 계산합니다.
        cost = graph[nodes[current_node_idx]][nodes[next_node_idx]] + \
            tsp_dp(graph, next_node_idx, visited_mask | (1 << next_node_idx))
        min_cost = min(min_cost, cost)

# [결과 기록 및 반환]
# 계산이 끝난 문제의 답(최소 비용)을 메모장에 기록합니다.
memo[(current_node_idx, visited_mask)] = min_cost
# 다음 재귀 호출을 위해 계산된 최소 비용을 반환합니다.
return min_cost

# 실행 및 결과 확인 (시작은 'A', 즉 인덱스 0에서)
cost_dp = tsp_dp(graph_simple, 0, 1)
print(f"동적 계획법 최단 거리: {cost_dp}")

실행 결과:
동적 계획법 최단 거리: 80

동적 계획법도 완전 탐색과 동일한 최단 거리 80을 찾아냈습니다! 코드는 조금 복잡해 보이지만, 완전 탐색보다 훨씬 효율적으로 동작합니다. 하지만 이 방법 역시 건물의 개수가 20개를 넘어가면 메모리와 시간 문제에 부딪히게 됩니다.

3단계. 외판원이 되어 서울대학교 캠퍼스를 누벼보아요!

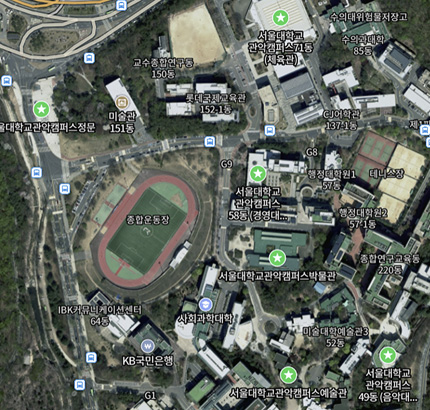
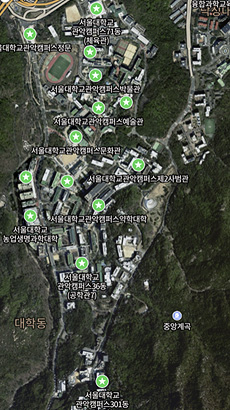
간단한 그래프에서는 세 알고리즘의 속도 차이를 체감하기 어렵습니다. 이제 실제 서울대학교의 주요 건물 14개로 구성된, 더 복잡한 그래프로 성능을 비교해 보겠습니다. 아래 사진은 서울대학교 주요 건물 14개를 선택한 네이버 지도 사진입니다.

표1 알고리즘 경로 비용 및 실행 시간 비교 표

완전 탐색	154	약 10~20분
동적 계획법	154	약 1.48초
Greedy MST 근사	154	약 0.002초

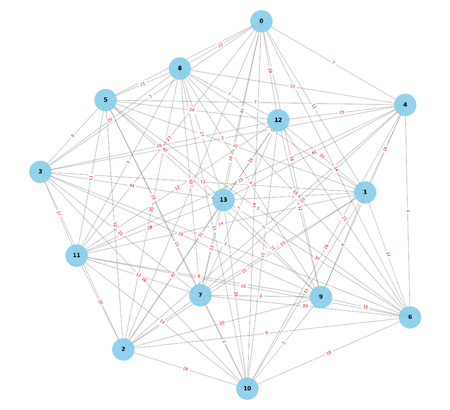
해당 건물을 노드로 하고 각 건물 사이의 도보 시간을 간선으로 하는 가중치 그래프를 그리면 아래와 같은 가중치 그래프가 그려집니다. 매우 복잡해보입니다. 91개(=14C2)개의 간선으로 이루어진 그래프이기 때문입니다. 노드에 매긴 값은 0번(서울대학교 정문) ~ 13번(서울대학교 301동)과 같이 고도가 낮을수록 낮은 값을 부여하였습니다. 이제 아래 그래프에 대해 앞서 소개한 3가지 알고리즘을 실행시킨 결과를 요약하면 다음과 같습니다.

완전 탐색으로 14개 건물을 모두 방문하는 경우의 수는 13! (팩토리얼)로, 약 62억 개에 달합니다. 컴퓨터가 1초에 약 천만(10,000,000) 개의 경로를 계산한다고 가정해 보더라도 623초 약 10분에 달하는 시간이 소요됩니다. 또한 만약 건물이 단 하나만 추가되어 15개가 되면 계산량은 14배로 늘어나 몇 시간이 걸릴 수 있기에, 복잡한 문제에서는 동적 계획법이나 근사 알고리즘과 같은 더 효율적인 접근 방식이 반드시 필요합니다.

반면 동적 계획법은 약 1.5초 만에 최적 경로의 총 이동 시간이 154분이라는 완벽한 답을 찾아냈습니다. 더 나아가 Greedy MST 근사 알고리즘은 매우 흥미로운 결과를 보여줍니다. 이번 사례에서는 최적해와 동일한 154분짜리 경로를 찾아냈지만, 실행 시간은 0.002초로 동적 계획법보다도 수백 배나 빨랐습니다.

근사 알고리즘이 찾은 경로는 최적 경로보다 더 긴 시간이 걸릴 수 있지만, 실행 시간은 수천 배나 빠릅니다. 만약 건물이 100개가 넘는 실제 물류 시스템이라면 어떨까요? 최적 경로를 찾기 위해 몇 분을 기다리는 것보다, 약간의 오차를 감수하고 몇 초 만에 효율적인 경로를 얻는 것이 훨씬 더 현명한 선택일 수 있습니다. 바로 이것이 정확성과 효율성 사이의 Trade-off⁷⁾에서 균형점을 찾는 공학적 사고의 핵심입니다.

결론: 효율적인 탐색, 공학적 사고의 힘!

이번 기사를 통해 우리는 서울대학교 캠퍼스를 예시로 삼아 외판원 문제와 다양한 경로 탐색 알고리즘을 살펴보았습니다. 완벽한 최적 해를 찾는 데 어려움이 있더라도, 더 빠르고 효율적인 근사적인 방법을 찾아내는 것 또한 공학적인 문제 해결 방식의 중요한 측면입니다. 이처럼 정확도와 속도의 Trade-Off 속에서 최고의 균형점을 찾는 고민은 비단 코딩에만 국한되지 않습니다. 제한된 시간과 자원 속에서 최선의 선택을 내려야 하는 것은 우리가 마주하는 많은 문제의 본질과도 같기 때문입니다. 여러분도 삶의 다양한 문제 속에서 자신만의 멋진 균형점을 찾아 나가길 응원하겠습니다.